（同）一張紙最多可以被（連續）對摺多少次？

先說結論：不止 7 次。

這個問題，以及通常伴隨着它的那一個標準答案，在許多對科學稍微有興趣的人當中傳開了好幾年。在這些人之中（當然，包括以前的我在內），只要你說得出這個問題的「標準答案」：「7 次」，人們就會認爲你因爲熟悉科學冷知識，而成爲一位對科學略知一二的科學愛好者。

但真正的科學愛好者，甚至是相關專業的學者，也許會有不同看法，因爲這個以不同語言傳遍世界各地（包括本人耳中）的傳言，其實不完全符合事實。

「但我聽說過一張紙真的不能被對摺超過 7 次，如果超過了它甚至會爆炸！」

不用急，其實我也聽過。而且許多 YouTube 影片（有些甚至被定位成「知識型影片」）都提到過這一點，而且還親自示範。舉個例子，以下在 YouTube 的點閱率高達 2 600 萬以上的影片是來自一個由某位擅於使用液壓沖床（hydraulic press）的人開設、並且以使用液壓沖床於各種不同物件作爲影片主題的頻道。他利用液壓沖床，「證明」了一張紙不僅不能被對摺超過 7 次，若要「嘗試超越」這個次數還會發生「嚴重的後果」。

即使不使用如此大陣仗的設備，若我們單純使用在學校和辦公室常見的厚度 60-80 gsm（grammes per square metre，每平方米 [公尺] 克 [公克]）的 A4 大小（長 29.7 厘米 [公分] 、寬 21 厘米 [公分]）白紙，並隨手直接對摺實測，我們也不難發現當到了第七次的時候，對摺的過程便已變得相當困難，更何況第八次？因此，我們就會很容易認爲一張紙真的只能最多被對摺 7 次。7 次已經是極限了。

不過，其實這並不能證明一張紙最多就只能被對摺 7 次、7 次真的是極限。

其實這個問題，並不如想象中單純⋯⋯

你是否有注意到，爲什麼在前面我提及的自己可以在家做的摺紙實驗，我對於所使用紙張的描述會如此地精確呢？

沒錯，這就是重點所在：其實一張紙最多可以被對摺幾次，是會受到紙張材質、寬度、厚度，還有摺紙的方式等因素影響。 換句話說，這個問題如果放在現實世界中探討以求在實際操作中一張紙可被對摺的極限次數的話，這便涉及了物理，也因此可以用物理知識來解釋。

首先，先說摺疊紙張的方式。眾所皆知，摺紙的方式有無數種，甚至因此衍生出摺紙藝術（origami）。不過，我們在此只考慮兩種相對有規律、也是許多人會直覺地想到的摺疊方式：

• 雙向交替對摺（alternate folding direction）：最直覺的對摺方式，即先將一張紙橫向對摺，然後縱向對摺，以此類推、交替進行。這也是多數人在只說「對摺」二字時，所指的摺疊方式。
• 單向對摺（single folding direction）：顧名思義，就是只沿一個方向對摺一張紙；爲了達到最大化可對摺的極限次數的效果，通常人們會選擇橫向對摺¹，因爲橫向對摺的話，可利用的「寬度」就是該紙張的長度，摺疊空間較大。

由於使用單向對摺的方式摺疊紙張時，每摺一次後所減少的紙疊寬度和雙向交替對摺比起來較多，因此使用單向對摺的方式所得到的極限次數會比在一模一樣的紙張使用雙向對摺方式來得少。

再來就是紙張的寬度和厚度了。根據美國西德州² A&M 大學（West Texas A&M University）現任物理系助教授 Christopher S. Baird 博士在該校網路專欄 Science Questions with Surprising Answers 的文章，紙張的厚度會影響該紙張被對摺的極限次數：在其他變數固定不變的情況下，紙張的厚度越薄，紙張可被對摺的極限次數就越多。Baird 博士也指出，一張紙可被對摺的極限次數，取決於紙張本身的厚度和寬度以及這兩者之間的關係：當對摺（摺疊）後的紙張高度（厚度）超過了它目前的寬度，由於僅剩的寬度（的一半）已無法超越目前的高（厚）度，因此也沒有可以繼續摺疊的空間；也就是說，該紙張已被摺疊到它的極限次數了。

Depending on the thickness and width of the paper, after a certain number of folds, the paper stack becomes thicker than it is wide. After that point, there simply is nothing left to fold, so the limit is reached.

（取決於紙張的厚度與寬度，當紙張被摺疊了幾次後，該疊紙的厚度便超過它目前的寬度了。在此之後，由於沒有可繼續摺疊的空間，它已達到[摺疊的]極限了。）

那麼根據這一點，一張紙無法繼續被對摺的臨界點，就是當被對摺後的紙疊高度等於它目前的寬度。

物理和數學往往脫不了關係，這個當然也不例外。因此，接下來的內容將涉及許多數學，請慎入。

在該文章中，Baird 博士也進行了數學計算，並且得出了一個公式，描述一張紙可被對摺的極限次數、紙張厚度與紙張寬度之間的關係。本人將在此儘量以簡略的方式重現這個運算過程。

無論是採用雙向交替對摺或單向對摺的方式，一張紙每被對摺一次，它的目前厚度就會是前一次的兩倍。若以 $n$ 表示對摺次數、$d$ 表示紙張厚度，這個現象可以被寫成這個數學表達式： $ 2^n d $。³

至於寬度的變化則是會因對摺方式的不同而有所差異：以長方形紙張來說，若只看其中一邊的寬度，雙向交替對摺的方式會讓紙張寬度每摺兩次減半，而單向對摺則是讓紙張寬度每摺一次減半。因此，若以 $l$ 表示紙張寬度，從中可以得出這兩個表達式：$\left(\frac{1}{2}\right)^{\frac{n}{2}} l$（雙向交替對摺）；$\left(\frac{1}{2}\right)^{n} l$（單向對摺）。

利用前面提到的對「無法繼續對摺的臨界點」的描述，我們可以得出兩個等式（equation）： $$ 2^n d = \left(\frac{1}{2}\right)^{\frac{n}{2}} l \text{（雙向交替對摺）;}$$ $$ 2^n d = \left(\frac{1}{2}\right)^{n} l \text{（單向對摺）。}$$

解出 $n$ 後，我們便得到最終的以 $n$ 爲主（subject）、涉及紙張寬度和厚度兩個變數的兩個公式： $$ n = \frac{1}{\ln 2^{\frac{3}{2}}} \ln{\frac{l}{d}}\approx 0.962 \ln{\frac{l}{d}} \text{（雙向交替對摺）;}$$ $$ n = \frac{1}{\ln 4} \ln{\frac{l}{d}} \approx 0.721 \ln{\frac{l}{d}} \text{（單向對摺）。}$$

其中，若按照雙向交替對摺版本的公式，並且代入普通 A4 大小白紙的寬度（$l$）與厚度（$d$）數值，以公釐（毫米，millimetre，mm）來說就是 $l = 210$ 以及 $d = 0.09$，就可以發現 $n$ 的值就會是 $ 7.4448 \ldots \approx 7$。這也解釋了爲什麼當我們使用普通的 A4 大小白紙時，最多就只能連續對摺 7 次。此外，既然有了公式，這也意味着透過改變寬度與厚度的數值，我們就可以得知哪一種紙張可以讓我們連續對摺它 7 次以上。

至於紙張的材質，它決定了一張紙可被對摺並且形成摺痕的難易度，影響了對摺該張紙所需的力與它被對摺後維持該狀態的韌性，也間接影響該張紙的可接受厚度。

更多的數學：這個現象，以及影響它的因素，甚至可以用數學定理來解釋！

若你以爲涉及數學的內容已經結束的話，那你就錯了，真正的數學主菜才剛開始。

在 2002 年以前（或者應該說到現在也是？），長久以來，「任何大小的紙張最多只能被連續對摺 7 次⁴」這個說法都被認爲是正確無誤的，畢竟不僅主流媒體（和後來的網路媒體）甚至一些學者都爲這個說法背書，人們在 A4 白紙上實測後也更加確信這個說法。

不過到了 2002 年，有一個人改變了這一切，並且利用數學證明了這個說法不正確，她就是來自美國加州²、當時還是 17 歲的美國高中生的 Britney Gallivan。

根據一篇爲 Britney Gallivan 的書作介紹的文章，Gallivan 投身這個摺紙以及數學證明活動的契機來自一堂數學課。當時，作爲該堂課的加分項，她與其他學生被要求試着將任何東西連續對摺 12 次。後來，Gallivan 成功使用一片金箔將它連續對摺 12 次，完成了當時被認爲不可能的任務。當然，她也嘗試過使用紙張進行連續對摺，並且已經成功用紙張連續對摺了 9 次、10 次，然後是 11 次。其中，她創下 11 次的紀錄時，使用的是一張非常長、厚度和衛生紙（廁紙）差不多的紙張，並且採用單向對摺的方式。她也發現，使用單向對摺的方式，比使用雙向交替對摺的方式更能節省紙張。

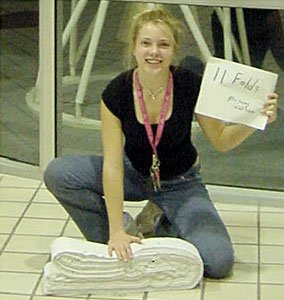
Gallivan 在努力達成連續對摺紙張 12 次的目標時，並沒有局限自己於實務上的嘗試，而是也同時嘗試利用數學證明，以找出若要達成連續對摺紙張任何次數的目標，所需要的紙張厚度與長度。最後，在 2002 年 1 月 27 日，她成功利用長度達 4 000 英尺（1 219 公尺或米）的衛生紙，創下了連續單向對摺紙張 12 次的紀錄，（再～一次地）打破了那個流傳已久並且一直被認爲正確無誤的傳言。換句話說，Gallivan 不僅在實際操作上打破了那個傳言，更進一步利用理論以數學證明的方式打破了那個迷思，也幫助人們找出了連續對摺次數背後的一個數學規律。

不僅如此，重點來了，Gallivan 也透過數學證明得出了兩個數學公式，讓人們知道要將一張紙連續對摺幾次，需要多長和多厚的紙張。這兩個數學公式被稱作摺紙定理（paper folding theorem），而該公式的證明也已收錄在美國密歇根大學（University of Michigan）的網站上。

在這兩個摺紙定理的公式當中，其中一個相對而言比較受人關注的公式是用於以單向對摺的方式對摺一張長方形紙條（paper strip）的情況下的。該公式的寫法如下： $$ L = \frac{\pi \cdot d}{6} \cdot \left( 2^n + 4 \right) \cdot \left( 2^n - 1 \right) $$ 其中，$L$ 代表該長方形紙條（或紙張）的長度（而非寬度）；$d$ 代表該紙條的厚度； $n$ 代表對摺次數。

而另外一個公式是用於以雙向交替對摺的方式對摺一張正方形紙張的情況下的⁵。該公式的寫法如下： $$ L = \pi \cdot d \cdot 2^{{\frac{3}{2}} (n-1)} $$ 其中，$L$ 代表該紙張的邊長⁵；$d$ 代表該紙張的厚度； $n$ 代表對摺次數。

讓我們在此試試看第二個公式。同上，以普通 A4 白紙爲例，同樣以公釐（mm）爲單位，代入 $L = 210 $ 以及 $d = 0.09$，最後得出的 $n$ 值爲 $ 7.3577 \ldots \approx 7 $，和前面的公式所得到的答案差不多，也符合實測的結果。因此，這個定理是成立的。

《線上整數數列大全》（The On-Line Encyclopedia of Integer Sequences®，OEIS®）甚至也收錄了由第一個公式除以 $π$ 和 $d$ 後並且代入遞增的自然數值的 $n$ 後所產生出的數列。從該數列可以看出，每一項的數值隨着數列進展的增加幅度非常大，因此這可以解釋爲什麼如果要試着增加一張紙可被對摺的極限次數，不僅需要使用很長的紙和很多材料，對摺難度也會隨着極限次數的增加而大幅度增加。

這個由 Gallivan 達成的「一張紙最多可被對摺的次數」已經被收錄在金氏世界紀錄（Guinness World Records，又譯爲「吉尼斯世界紀錄」）當中。她也爲了此項創舉寫了 How to Fold Paper in Half Twelve Times (An “Impossible Challenge” Solved and Explained) 這本解釋她創下這個紀錄的心路歷程的書，並在同（2002）年出版。不過現在這本書已經絕版，因此除非有備份或者曾經看過這本書，否則裡頭的內容就無法得知了。

雖說金氏世界紀錄收錄的是 Gallivan 創下的 12 次紀錄，但其實在 2011 年，一群來自美國麻省²聖馬克高中（St. Mark’s School）的學生在麻省理工學院（Massachusetts Institute of Technology，MIT）校舍內曾經創下了以單向對摺的方式連續對摺紙張 13 次 的紀錄。他們花了長達 7 小時，使用了比之前 Gallivan 使用的還要長上許多的衛生紙（長達約 10 英里，或約 16 093 公尺！）達成了該紀錄。以下影片描述了他們創下該紀錄的過程。

結語

在 Gallivan 創下對摺紙張的世界紀錄，並且得出了那兩個數學公式之前，應該很少人想過所謂的 7 次傳言就只是個傳言，而且應該幾乎沒有人想過一個隨性的摺紙動作，背後竟然有數學規律存在。

雖說這應只能算是個數學冷知識，但是這也證明了有時候在尋求一個問題的答案時若看得不夠全面，不僅會錯失尋得更深一層規律的機會，也會讓似是而非的說法一直被流傳下去。而且，生活中真的幾乎是 「處處有數學」，一個不起眼的小動作背後竟也可以利用數學找出它的規律。

那麼，會不會有即使利用數學也無法解釋的某種動作、規律或自然現象呢？我相信肯定是有的，但數學家們一定會想盡辦法「發明」出新的數學語言來解釋它，或者是乾脆創一個新公理來試圖解釋它（如果他們有信心的話）。

資料來源、延伸閱讀：

• ScienceABC 網站文章⁶

• Wolfram MathWorld 題爲 Folding 的文章

• Britney Gallivan 維基百科文章

• 論文 Introducing Robotic Origami Folding

• Britney Gallivan 的書 How to Fold Paper in Half Twelve Times (An “Impossible Challenge” Solved and Explained) 介紹文章

• 維基百科文章 Mathematics of Paper Folding

• 摺紙定理（單向對摺）

• 摺紙定理（雙向交替對摺）